英语中的有趣现象

2019-10-19    340 words    2 minute read  
# Linguistics # english # mathematica

有哪些英语单词倒过来是另一个单词？

DictionaryLookup[x__ /; DictionaryWordQ@StringReverse@x]

有哪些英语单词是回文的？

DictionaryLookup[x__ /; x === StringReverse@x]

有个慢一点的方法, 但是可以短一点

DictionaryLookup[x__ /; PalindromeQ@x]

哪两个字母不可能连在一起？

https://www.zhihu.com/question/25908268

英文各字母使用频率？

https://www.zhihu.com/question/23111432

英语单词 26 个首字母出现概率各是多少？

https://www.zhihu.com/question/30077599

英语单词哪个字母出现频率最高?

https://www.zhihu.com/question/19805834/answer/67555450

Read more...

TF 卷积的 pad 算法

2019-10-06    740 words    4 minute read  

二、tf的padding有两个值，一个是SAME，一个是VALID

以下展示卷积三种模式的不同之处

其实这三种不同模式是对卷积核移动范围的不同限制。设 image的大小是7x7，filter的大小是3x3。

Valid Mode

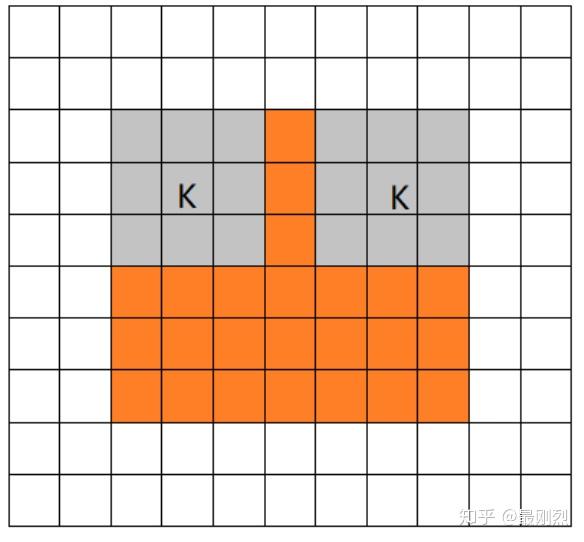
当filter全部在image里面的时候，进行卷积运算，可见filter的移动范围较same更小了。

  • 输入图片大小: W*W

  • Filter大小:

  • 步长: S

  • padding的像素数: p

N = (W- F+ 2P)/S+1

输出大小为NN

如果padding设置为SAME，则说明输入图片大小和输出图片大小是一致的，如果是VALID则图片经过滤波器后可能会变小。

padding = "VALID"输入和输出大小关系如下：

$$n_{\text {output}}=\left[\frac{n_{\text {input}}-f+1}{s}\right]$$

conv2d的VALID方式不会在原有输入的基础上添加新的像素（假定我们的输入是图片数据，因为只有图片才有像素），输出矩阵的大小直接按照公式计算即可。

Same Mode

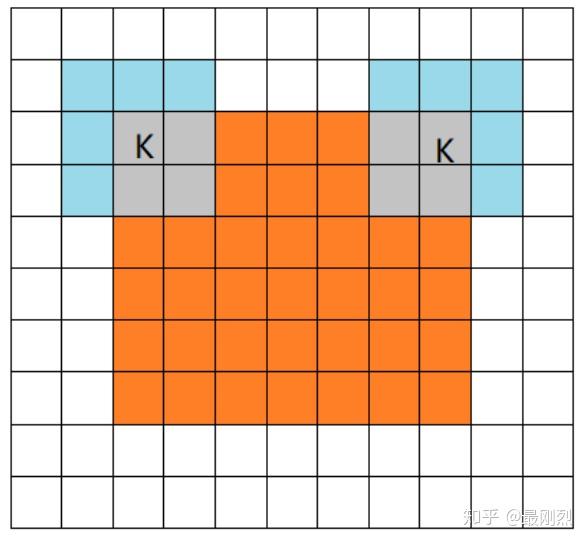
当filter的中心(K)与image的边角重合时，开始做卷积运算，可见filter的运动范围比full模式小了一圈。注意：这里的same还有一个意思，卷积之后输出的feature map尺寸保持不变(相对于输入图片)。当然，same模式不代表完全输入输出尺寸一样，也跟卷积核的步长有关系。same模式也是最常见的模式，因为这种模式可以在前向传播的过程中让特征图的大小保持不变，调参师不需要精准计算其尺寸变化(因为尺寸根本就没变化)。

padding = "SAME"输入和输出大小关系如下：输出大小等于输入大小除以步长向上取整

$$n_{\text {output}}=\left[\frac{n_{\text {input}}}{s}\right]$$

在高度上需要pad的像素数为：
pad_needed_height = (new_height [Dash] 1) * S + F - W

根据上式，输入矩阵上方添加的像素数为：
pad_top = pad_needed_height / 2 （结果取整）

下方添加的像素数为：
pad_down = pad_needed_height - pad_top

以此类推，在宽度上需要pad的像素数和左右分别添加的像素数为
pad_needed_width = (new_width [Dash] 1) * S + F - W
pad_left = pad_needed_width / 2 （结果取整）
pad_right = pad_needed_width [Dash] pad_left

Full Mode

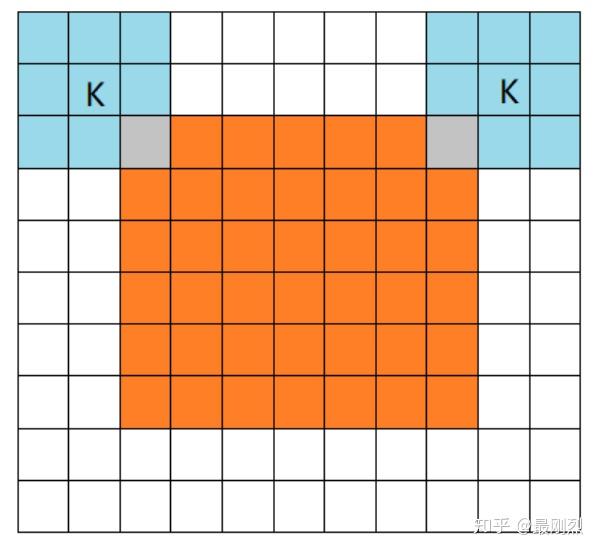
橙色部分为image, 蓝色部分为filter。full模式的意思是，从filter和image刚相交开始做卷积，白色部分为填0。filter的运动范围如图所示。

Read more...

CV 模型的标准化

2019-03-09    629 words    4 minute read  
# Deep Learning # Computer Vision

序数 or 偏移

深度学习第一个坑就是从 0 编号还是从 1 编号.

虽然大多数框架都选择了从 0 开始, 但我还是得说这是反人类的.

从零开始计数一般用在偏移中, 比如内存, 每个字节是几偏移.

但是深度学习就不一样了, 比如标签, 我们通常说是第几个.

这是序数啊, 从来不会有第 0 个这么奇葩的说法.

依次交换0维3维1维2维, 我是无力吐槽了, 你和谁的偏移量0312, 是给人看的吗你这...

推导不能, 反正全给他 +1 就得了.

RGB or BGR

这个问题无关痛痒,

我不知道重排首个卷积核的话怎么写, 理论上也是可以的.

NCHW or NHWC

我是真的不知道 NHWC 的优点在哪, 难道硬件底层更加合适吗?

NCHW 下取第一张图片就是 img[1], NHWC 则要写 img[:,:,:,1], 何苦啊这是...

左下系 or 左上系

左上系的支持者理由是图片即矩阵, 第一行第一个像素就是 img[:,1,1]

用左下系就要写 img[:,1,-1], 多了个负号

哦对了, 某些从零开始计数的垃圾玩意儿压根没法用 -1 表示倒着数.

(所以为什么不规定为矩阵从下开始数...

但是不管怎么说数学老师当初教我就是左下建系, 所以这样更符合习惯.

解决方案

遇到左下系就转换为左上系

施加变换 $y -> 1-y$ 即可, 记得目标检测里 {y_

\min{}
} 和 {y_
\max{}
} 对调一下.

右手系 or 左手系

如果 2D 用了左上系, 3D 用左手系似乎是天经地义的.

当我们还是习惯朝对我们的平面是 0, 越往里面越远不是, y 轴越大离摄像头就越远, 景深就越深

不管怎么说这也是习惯问题罢了, 不是很重要.

解决方案

遇到左手系就转换为右手系

乘上变换矩阵 $\begin{bmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\\\end{bmatrix}$ .

Read more...

Windows 全深度学习环境安装

2019-03-07    549 words    3 minute read  
# Deep Learning # windows # torch # tensorflow # mxnet

下载地址: https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/

别乱点直接一路确认, 安装很慢, 可以去看会儿电影

安装完了就建一个新的隔离环境

conda create -n deeplearning python=3.7
conda activate deeplearning

然后添加一些中心包服务器, 比如 conda-forge 是一定要有的, 不然很多包都下不到.

conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main/
conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/conda-forge/
conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/pytorch/
conda config --add channels willyd
conda config --set show_channel_urls yes
conda config --show channels

不要添加那个叫 free 的, 里面都是老的不能用的玩意儿, 如果添加了那最好移除.

conda config --remove channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/

最后直接一条命令安装即可

conda install tensorflow keras caffe-cpu pytorch-cpu -y
pip install mxnet

千万不要加 -c 除非你住在墙外.

然后由于 conda 实在是非常非常的慢, 现在可以去睡一觉

等一觉醒来就可以愉快的使用各大深度学习环境啦

当然可能由于网络连接问题中断, 那没办法了, 一遍不行就只能再装一遍了

最后还可以装一些常用的模型库

比如 torchvision-cpu gluoncv 啥的

Read more...

寻找数列万能公式

2018-03-24    2839 words    15 minute read  
# #

自学生时代以走来, 总是对公式有种迷信, 无数伟大人物, 将一生成就凝练为公式造福后人, 解题只需记住并活用公式即可.

久而久之, 就对一些老师没有讲过的东西怀有好奇, 比如素数有没有公式? 自然数倒数和有没有公式? 有没有万能的数列公式?

当然数学中抛开定义谈问题都是耍流氓, 函数你承不承认是公式? 那我随手画条线把所有的点连起来这叫图像函数吧, 这算不算公式?

所以数学上什么才叫公式呢?

初等函数

素数自然是有公式的, 有好几个, 一般长这样:

$$p_n=1+\sum_{m=1}^{2^n}\left\lfloor \sqrt[n]{\left\lfloor n\biggl/\sum_{k=1}^m {\left\lfloor \cos^{2} \lfloor \pi\dfrac{(k-1)!+1}{k} \rfloor \right\rfloor} \right\rfloor} \right\rfloor$$

自然数倒数和也是有公式的, $\sum_{n>1}=H_n$

当然你觉得这不叫公式也无所谓, 因为这的确不是一般意义上的公式.

所谓的公式能分为以下五个等级:

  1. 只用加减乘除的公式叫做 算数表达式(Arithmetic expressions).

  2. 加入幂, 开根之后叫做 代数表达式(Algebraic expressions).

  3. 允许使用初等函数的公式叫做 封闭形式(Closed-form expressions), 也可以叫初等表达式.

  4. 允许使用级数算符的公式叫 解析形式(Analytic expressions), 其中级数要求收敛, 不能是形式幂级数.

  5. 剩下的统称为数学定义式(Mathematical expressions), 允许使用包括极限、微分与积分算符在内的一切数学符号, 级数可以是单点收敛的形式幂级数, 甚至式子不必用等式定义, 直接说是某个方程的解.

平常所谓的公式一般是第三个等级, 允许使用一切初等函数. 当然没学过函数那就是第二级, 理工科大学生自行把公式的定义提到第四级, 我肯定已经到了第五级了喽,lol...

基本初等函数是由刘伟尔钦定的函数集合, 只有反对幂三指常六种, 在这之外的函数都被称为特殊函数, 没有高等函数这种东西的...

基本初等函数的复合叫做初等函数.

显然一般的分段函数, 取整函数这些都不是初等函数. 绝对值函数倒也是初等函数, 这是特殊的分段函数嘛...

分段函数

用分段函数我们有个无耻的办法给出万能公式, 大不了每个点上给的定义呗

什么, 你说太无耻了? 那好, 大不了两个点之间连起来啊,233...

不说笑了, 我们知道两点确定一条直线, 或者可以等价的说成两个点确定一条一次函数曲线.

那我们固定两端的点, 然后把曲线扭动变成二次函数, 让它贴合第三个点, 可以吗?

这叫样条插值, 用三次曲线就叫三次曲线样条插值, 也可与不用多项式, 用别的, 比如B样条插值就是用贝塞尔曲线(BezierCurve).

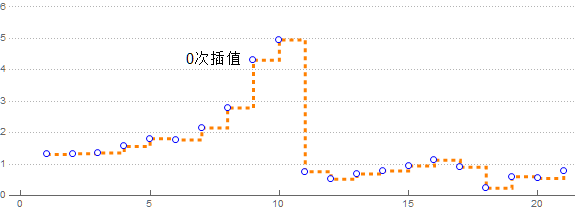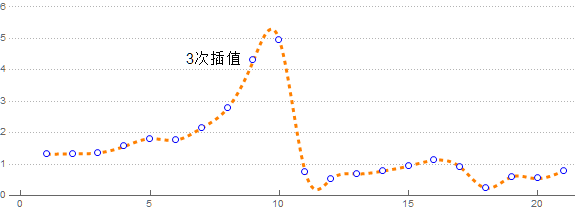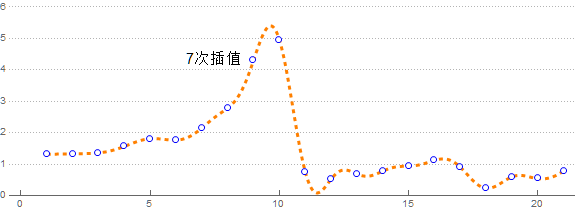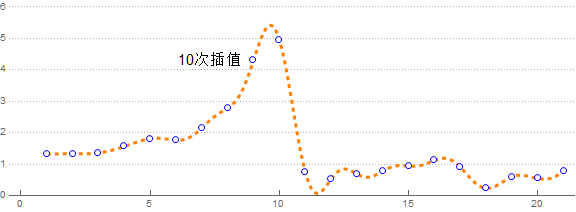
![](https://i.loli.net/2018/03/24/5ab63a46384a5.gif)

那不断提升次数会怎么样呢?

插值函数

$n$ 个点最多能确定了一个 $n-1$ 次的多项式.

那么用待定系数法, 解一个 $n-1$ 元方程即可, 于是可以用矩阵求解.

$$\begin{cases} y_1 = a_0 + a_1x_1 + a_2x_1^2+\cdots+a_nx_1^n\\ y_2 = a_0 + a_1x_2 + a_2x_2^2+\cdots+a_nx_2^n\\ y_3 = a_0 + a_1x_3 + a_2x_3^2+\cdots+a_nx_3^n \\ \cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots \\ y_n = a_0 + a_1x_n + a_2x_n^2+\cdots+a_nx_n^n \end{cases}$$

$$ \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots\\y_n \end{pmatrix} = \begin{pmatrix} 1 & x_1 & x_1^2 &\cdots&x_1^n\\ 1 & x_2 & x_2^2 &\cdots&x_2^n\\ 1 & x_3 & x_3^2 &\cdots&x_3^n\\ \vdots&\vdots&\vdots&\ddots&\vdots&\\ 1 & x_n & x_n^2 &\cdots&x_n^n\\ \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots\\a_n \end{pmatrix} $$

或者简写成:

$$\vec{y}=X\vec{a}$$

两边左乘逆矩阵 $X^{-1}$ 即可, 同时 $|X|\ne0$ , 说明方程只有唯一解. 也就是说这样的多项式是唯一的.

解出来后原来的式子可以重写为:

$$P(x):=\sum_{j=0}^{k}y_{j}\prod _{0\leq m\leq k}^{m\neq j}{\frac {x-x_{m}}{x_{j}-x_{m}}}$$

手解这个也太丧病了点, 编程大法好...

![](https://i.loli.net/2018/03/24/5ab63a461dd88.png)

生成函数

生成函数就是另一种概念上的东西了, 我们知道一个函数在原点的多项式级数展开被称为麦克劳林展开,且这样的展开是唯一的.

也就是说, 一个函数唯一确定了一个系数数列. 反过来, 一个数列也唯一确定了一个函数呀!

比如 $G(x)=e^x=\sum _{n=0}^{\infty }{\dfrac {x^{n}}{n!}}\quad \forall x\in\mathbb{R}$ .

那么可以记 $g_n=[z^n]G(x)=\dfrac{1}{n!}$ , 此时 $G(x)$ 就被称为 $g_n$ 的生成函数.

对一个有限的数列而言, 它的生成函数就是个 $n$ 次多项式.

生成函数并非数列换个写法这么简单, 一方面生成函数相当于定义了一种新的运算, 大大扩展了能表示的数列的种类.

比如高次求和中出现的伯努利数, 本身只有递推计算式, 没有初等表达式, 但它的生成函数是初等的.

$$\frac{B_n}{n!}=[z^n]\left(\frac{z}{e^z-1}\right)$$

更重要的是, 生成函数事实上蕴含了数列本身的一切信息.

比如数列和就是 $G(1)$ , 其他什么数列极限数列的渐进性质都在里面了, 数列通项什么的已经无所谓了.

可以想象, 即便如此, 还是会有很多的式子无能为力, 生成函数的另一个强大的地方就是化离散为连续, 使用微积分, 复分析乃至更强大的方法来研究.

后记

初学者总是觉得通项公式是万能的东西, 有了这个一切都能迎刃而解.

不过你看素数有公式吧, 各种有关素数的猜想都没秒杀了吗?

就算是高考题中, 不用解出通项也能搞定的题多了去了, 有的出题老师压根就没准备让你解出通项...

经典的比如 $a_1=1;a_{n+1}=\dfrac{1}{a_n}+a_n$ , 这么多年了, 总是能隔三差五看到有人试图求其通项.可原题明明要你证不等式啊!

就算是从业者中竟然也有人对 N-S 方程暂没有解析解感到恐惧, 迷信公式看轻数值, 搞得好像有了解析解就不用显卡算了一样, 人类能直接殖民月球了.

也许是因为公式是一种物理实在吧, 能给人以安全感.

数学到了一定层次, 都是在与抽象的不可名状物战斗了. 你是航天员, 要探索人类的未知领域, 在太空还能用地面那一套吗?

万能公式存在也不存在, 一切所谓的公式不过是概念的封装. 人最重要的是人的品格而非名字, 函数也是如此, 叫什么重要吗? 有没有公式重要吗?

data=BlockRandom[SeedRandom[42];Table[Exp[-3 x/(2+ x+x^2)]+RandomReal[{-.5,.5}],
  {x,-10,10}]
];
p[i_]:=ListLinePlot[Labeled[data,Text@Style[ToString@i<>"次插值",15],{Scaled[0.35],Above}],AspectRatio->1/3,
  InterpolationOrder->i,PlotRange->{0,6},
  PlotStyle->Directive[Orange, Dashed],PlotTheme->"Business",
  Mesh->Full,MeshStyle->Blue,ImageSize->Large
];
Export["万能公式_1.gif",p/@Range[0,10],
  "AnimationRepetitions"->Infinity,
  "DisplayDurations"->1
]
Read more...

21道犹太棺材题(上)

2018-03-06    371 words    2 minute read  
# Math # hard problems

Question 1

求解如下不等式, 其中$x$ 为正实数.
$\displaystyle{x(8\sqrt{1-x}+\sqrt{1+x})\leq11\sqrt{1+x}-16\sqrt{1-x}}$

Question 2

找出所有的函数 F(x): R→R ，使得对于任意两个实数 x1 、 x2 都满足 F(x1) – F(x2) ≤ (x1 – x2)2 。

不等式可以变为 (F(x1) – F(x2)) / |x1 – x2| ≤ |x1 – x2| ，于是我们立即可知，对于任意实数 x2 ，函数在 x2 处的导数都为 0 。因此， F(x) 是常函数。

Question 3

找出所有的函数 F(x): R→R ，使得对于任意两个实数 x1 、 x2 都满足 F(x1) – F(x2) ≤ (x1 – x2)2 。

Question 4

给定三角形 ABC ，用尺规作图找出 AB 上的一点 K 以及 BC 上的一点 M ，使得 AK = KM = MC 。

Question 5

求解实数方程:
$\displaystyle{2 \sqrt[3]{2 y-1} = y^3 + 1}$

答案：令 x = (y3 + 1) / 2 ，原式就变成了 y = (x3 + 1) / 2 。如果令函数 f(t) = (t3 + 1) / 2，你会发现 x 和 y 同时满足 f(x) = y 和 f(y) = x 。然而函数 f(t) 是严格单调递增的，因此 x 一定等于 y 。
于是，方程就变成了 y3 – 2y + 1 = 0 。等式左边可以变为 (y3 – y2) + (y2 – y) – (y – 1) ，进而分解为 (y – 1)(y2 + y – 1) 。于是得到方程的三个解： y = 1 和 y = (- 1 ± √5) / 2 。

Question 6

Question 7

Read more...

常见同分异构体计数

2018-03-04    4036 words    21 minute read  
# Chemistry # Combinatorics

引言

计算

烷基自由基计数

我们从卤代烃$C_nH_{2n+1}X$ 开始, X是卤素, 当然也可以是别的取代基.

Planarisomers

设 Free radicals count ,$\mathtt{Fr}(x)$

三个取代基的置换群若不考虑手性为 S_3 ;若考虑手性为 A_3 

\cong{}
\mathbb{\Z{}}
_3

$$\mathbb{Z}(\mathcal{S}_3)=\frac 16 (2s_3+3s_2s_1+s_1^3)$$

补上剩下的一个碳

$$\begin{aligned} A(x)&=1+x\mathbb{Z}[\mathcal{S}_3,A(x)]\\ &=1+\dfrac{x}{6}[A^3(x)+3A(x)A(x^2)+2A(x^3)] \end{aligned}$$

当然这个函数方程怎么展开是个大问题, 我们可以使用附录中级数的复合与反演来解决.

A[z_]:=Evaluate@Normal@Fold[
    Series[1+z/6(#^3+3# ComposeSeries[#,z^2+O[z]^#2]+2 ComposeSeries[#,z^3+O[z]^#2]),{z,0,#2}]&,
    1+O[z],Range@Floor@n
];

Stereoisomers

三个取代基的置换群若考虑手性为循环群 $\mathcal{C}_3$

$$\mathbb{Z}(\mathcal{C}_3)=\frac13(s_1^3+2 s_3)$$

A[z_]:=Evaluate@Normal@Fold[
    Series[1+z/3(#^3+2 ComposeSeries[#,z^3+O[z]^#2]),{z,0,#2}]&,
    1+O[z],Range@Floor[n/2]
];

烷烃计数

接下来考虑从烷基自由基组合生成烷烃 $C_nH_{2n+2}$

$$p^*-q^*+s=1$$

点的等价类数-边的等价类数+对称边数=1

碳的不同标记方法数-键的不同标记方法数+对称键数=1

let Alkane Count,$\mathtt{Ac}$ 

\mathtt{\Ac{}}

(z)=P(z)-Q(z)+S(z)

Planarisomers

$$\begin{aligned} P(x)&=x\mathbb{Z}[\mathcal{S}_4,A(x)]\\ &=\frac{1}{24}x(A^4(x)+6A^2(x)A(x^2)+3A^2(x^2)+8A(x)A(x^3)+6A(x^4))\\ Q(x)&=\mathbb{Z}[\mathcal{S}_2,A(x)-1]\\ &=\frac 12((A(x)-1)^2+A(x^2)-1)\\ S(x)&=A(z^2)-1 \end{aligned}$$

AlkaneSeries[n_Integer]:=Block[
    {A,P,Q,S,G},
    A[z_]:=Evaluate@Normal@Fold[
        Series[1+z/6(#^3+3# ComposeSeries[#,z^2+O[z]^#2]+2 ComposeSeries[#,z^3+O[z]^#2]),{z,0,#2}]&,
        1+O[z],Range@Floor[n/2]
    ];
    P[z_]=z CycleIndexPolynomial[SymmetricGroup[4],Array[A[z^#]&,4]];
    Q[z_]=CycleIndexPolynomial[SymmetricGroup[2],Array[A[z^#]-1&,2]];
    S[z_]=A[z^2];
    Series[P[z]-Q[z]+S[z]-1,{z,0,n}]
];

Stereoisomers

同样的 $p^*$ 由对称群$\mathcal{S}_4$ 变为交错群$\mathcal{A}_4$ .

$$\mathbb{Z}(\mathcal{A}_4)=\frac{1}{12}(s_1^4+8 s_3 s_1+3 s_2^2)$$

$$Q(x)=\mathbb{Z}[\mathcal{A}_4,A(x)]=\frac{1}{12}\left(8 A\left(z^3\right) A(z)+3 A\left(z^2\right)^2+A(z)^4\right)$$

AlkaneSeries[n_Integer]:=Block[
    {A,P,Q,S,G},
    A[z_]:=Evaluate@Normal@Fold[
        Series[1+z/3(#^3+2 ComposeSeries[#,z^3+O[z]^#2]),{z,0,#2}]&,
        1+O[z],Range@Floor[n/2]
    ];
    P[z_]=z CycleIndexPolynomial[AlternatingGroup[4],Array[A[z^#]&,4]];
    Q[z_]=CycleIndexPolynomial[SymmetricGroup[2],Array[A[z^#]-1&,2]];
    S[z_]=A[z^2];
    Series[P[z]-Q[z]+S[z]-1,{z,0,n}]
];

苯环

pg = GroupDirectProduct[AlternatingGroup@5, CyclicGroup@2];
A[z_, i_] := Evaluate[#^i & /@ (1 + a + b + c + d)]
CycleIndexPolynomial[pg, Array[A[z, #] &, 60]];
Coefficient[%, a b c d]

附录

旋转群与指标多项式

S,C,A,D

级数复合与反演

拉格朗日反演, 比起比较两边系数高到不知道哪里去了.

群直积与积群

GroupDirectProduct[g1_,g2_]:=With[
    {order1=GroupOrder@g1,order2=GroupOrder@g2,r,pd},
    r=Thread[Range[order2]->(order1+Range[order2])];
    pd=Outer[PermutationProduct,GroupElements[g1],GroupElements[g2]/.r];
    PermutationGroup@Flatten@pd
]

我刚开始以为Mathematica没有计算群直积的函数, 然后写了个GroupDirectProduct.

后来才发现确实没有这个函数, 因为群直积居然划分在群属性里.

GroupDirectProduct[AlternatingGroup@5,CyclicGroup@2]
FiniteGroupData[{"DirectProduct",
    {
        {"AlternatingGroup",5},
        {"CyclicGroup",2}
    }
},"PermutationGroupRepresentation"]
Read more...